dx(absolute values to see negative edges)
dy(absolute values to see negative edges)
Magnitude
Binarized magnitude. Threshold=0.322
1 Detect edges with finite difference operator.
2 Image sharpening.
3 Combining two frequencies of different images.
4 Blending images.
I used the following matrices as my finite difference operator. dx = [[-1, 1], [0, 0]], dy = [[-1, 0], [1, 0]]. This matrices find the diffrence between two neighbouring pixels, so if the change in pixels is big, the gradient is big. Second column/row are used as padding to keep dimensions consistent. Magnitude of the gradient is the square root of sum of squares between two images convolved with finite difference operators. mag = SQRT((IM*dx)^2 + (IM*dy)^2)
To get better results we can run image through gaussian filter, this will smooth it and remove some of the noise. I used gaussian with size 13 and sigma = 2.
As we can see we got an image with better defined edges. In the first example there were some random holes in the outline of the person, and using DoG filter fixed that. As we can see on the magnitude picture, the noise is reduced drastically, allowing us to use higher threshold value.
We can convolve dX and dY operators with our gaus operator to convolve image with that single matrix instead of Gaussian and dX/dY separately.
As we can see this produces same results.
To sharpen the image we can add some of its higher frequencies to the original image. To find high frequencies of the image I ran image through Gaussian filter and subtracted the result from the original image. I then added the result of this subtraction to the original image to get "sharpened" image. Let K be the number of times I added higher frequencies to the original.
I now blurred an image of the forest and then sharpened it to compare to original:
Comparison of original and sharpened image:
Since some information was lost after running Gaussian filter we cannot reconstruct image fully. However we can see that after sharpening the image looks more similar to the original than the blurry one.
We can combine low frequencies of one image with high frequencies of another to get image which looks like first image from afar, but second from up close
Derek and nutmeg:
Bells and whistles: I am combining images with color and I noticed that it works best if low frequency image is black and white and high frequency is colored.
Failure, I think the white background made it hard to see the the edges of the cat face, this is because I am using clamped add, as my high frequencies have black background and not a transparent one:
Wolfman or smth idk:
Fourier analysis
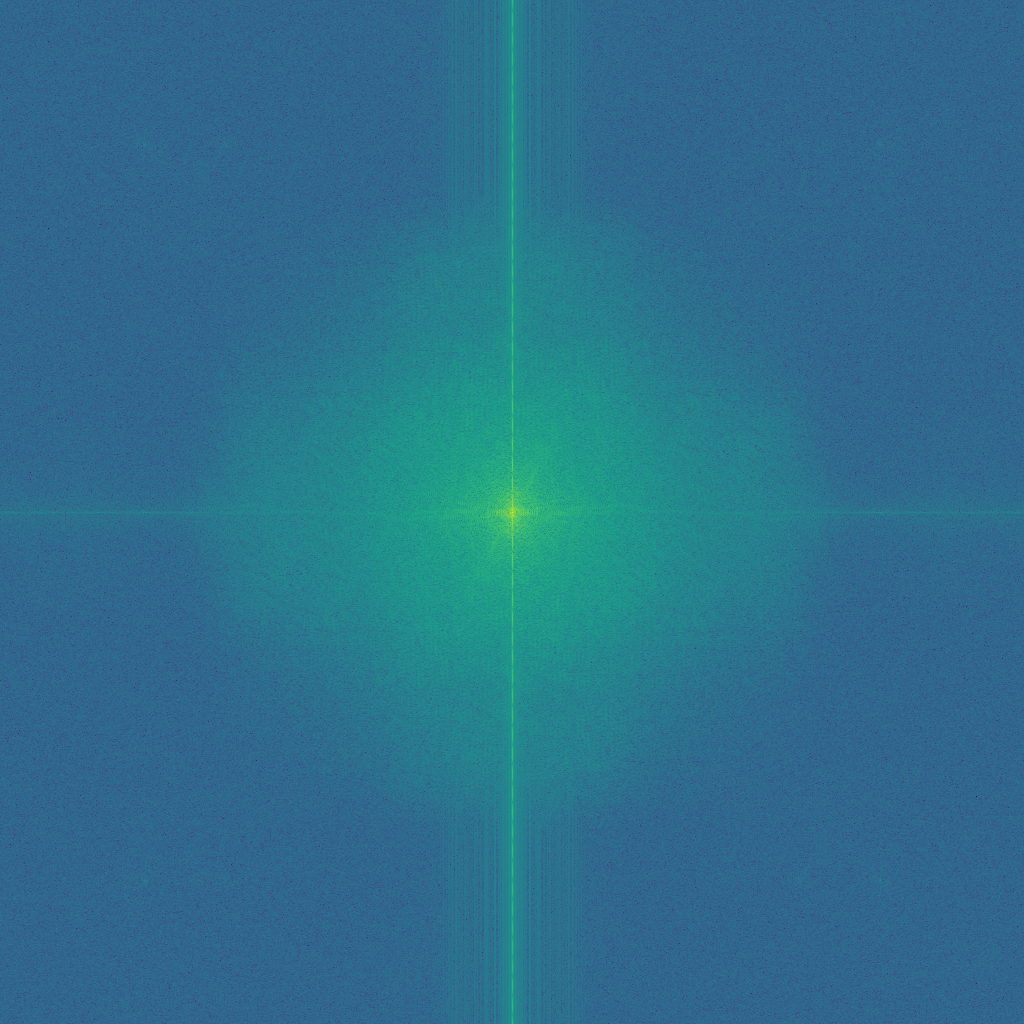
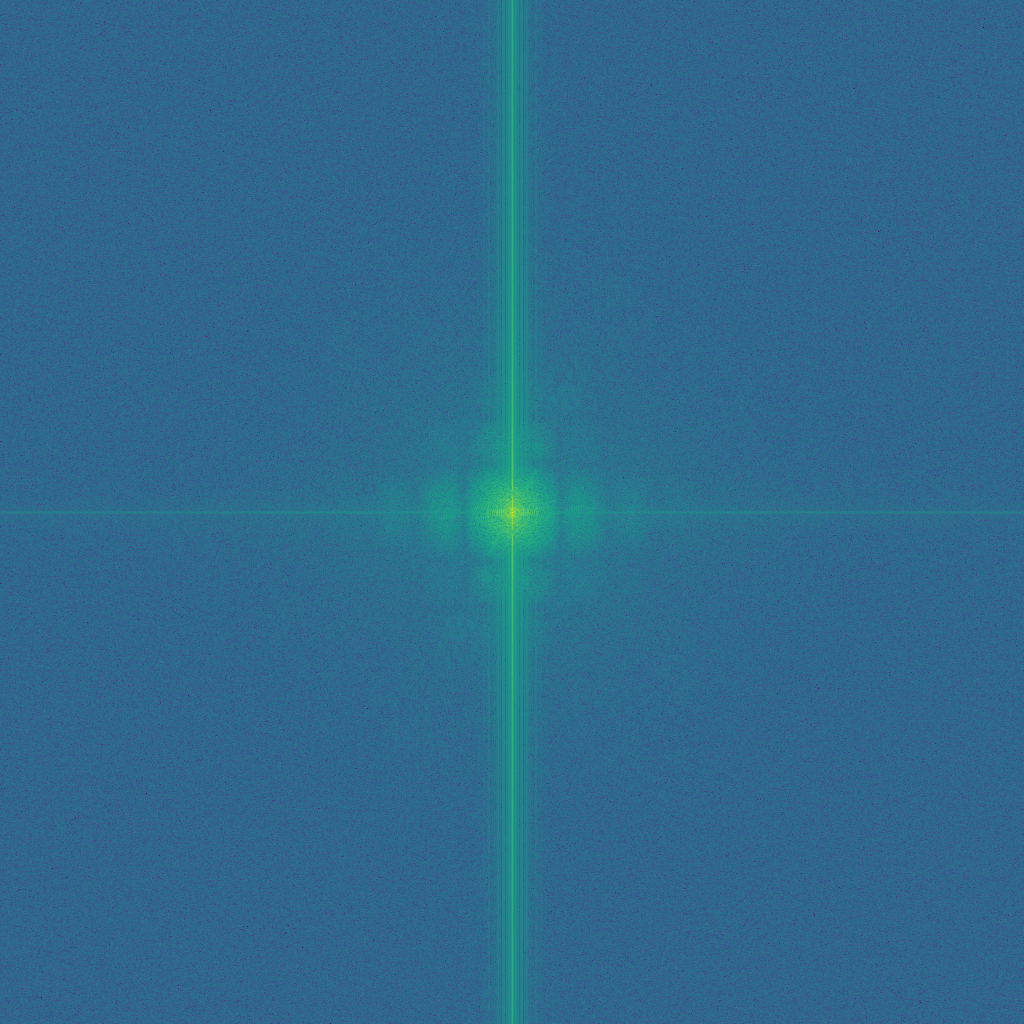
Pogrenade, an example where both colored images look good:
Gaussian stack is a list of images with Gaussian filter applied to them, each subsequent image has had filter applied 1 more time than the previous one. Laplacian stack takes 2 images from Gaussian stack and subtracts them, this extracts the high frequencies between those two images.
Here are my results of creating Laplaccian and Gaussian stacks (Laplaccian images are normalized for viewability reasons), apple:
Orange:
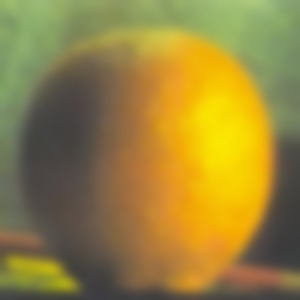
To get a smooth blend between two images we can blend their frequencies at each level of Laplaccian stack, using mask which has been blurred progressivelly more at each level. This way sharper details will have a smaller seam, while higher level details will blend over bigger distance.
Below are levels of mask, apple * mask, orange * (1-mask), apple * mask + orange * (1-mask) (*normalized for viewability considerations):
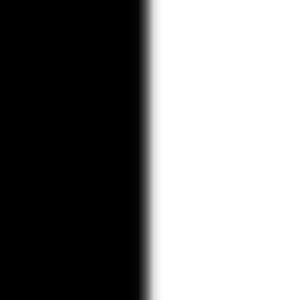
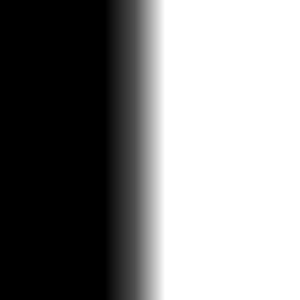
Curtle stacks:
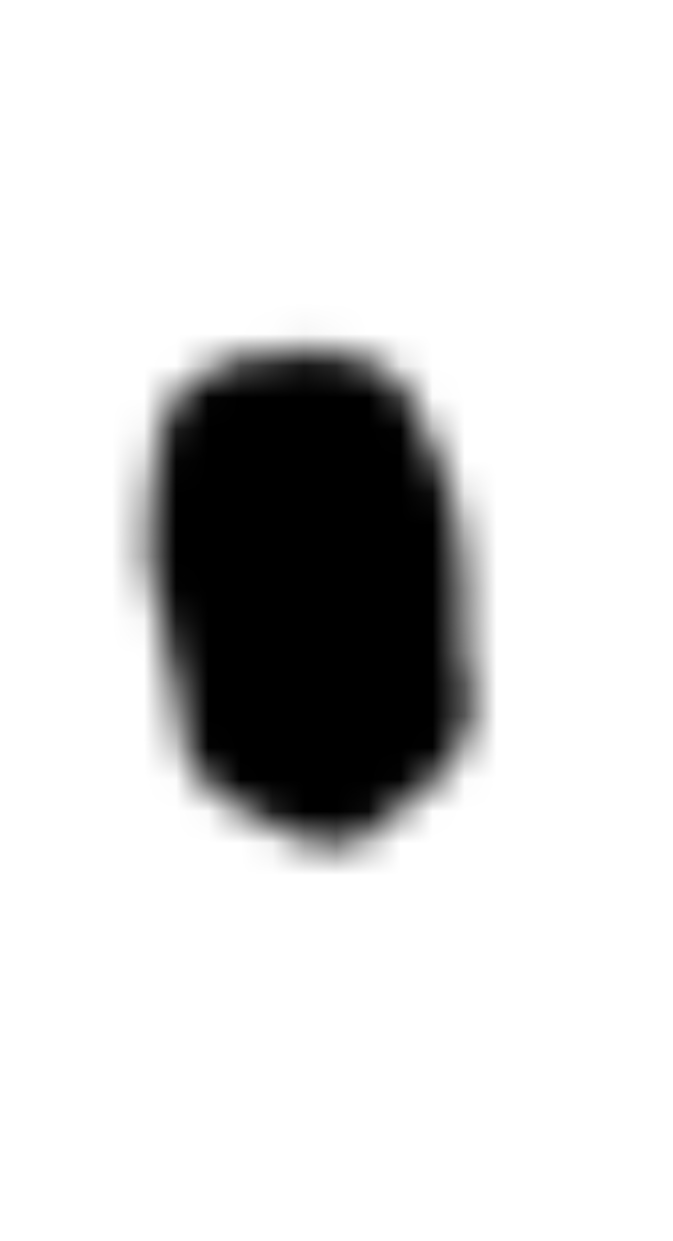
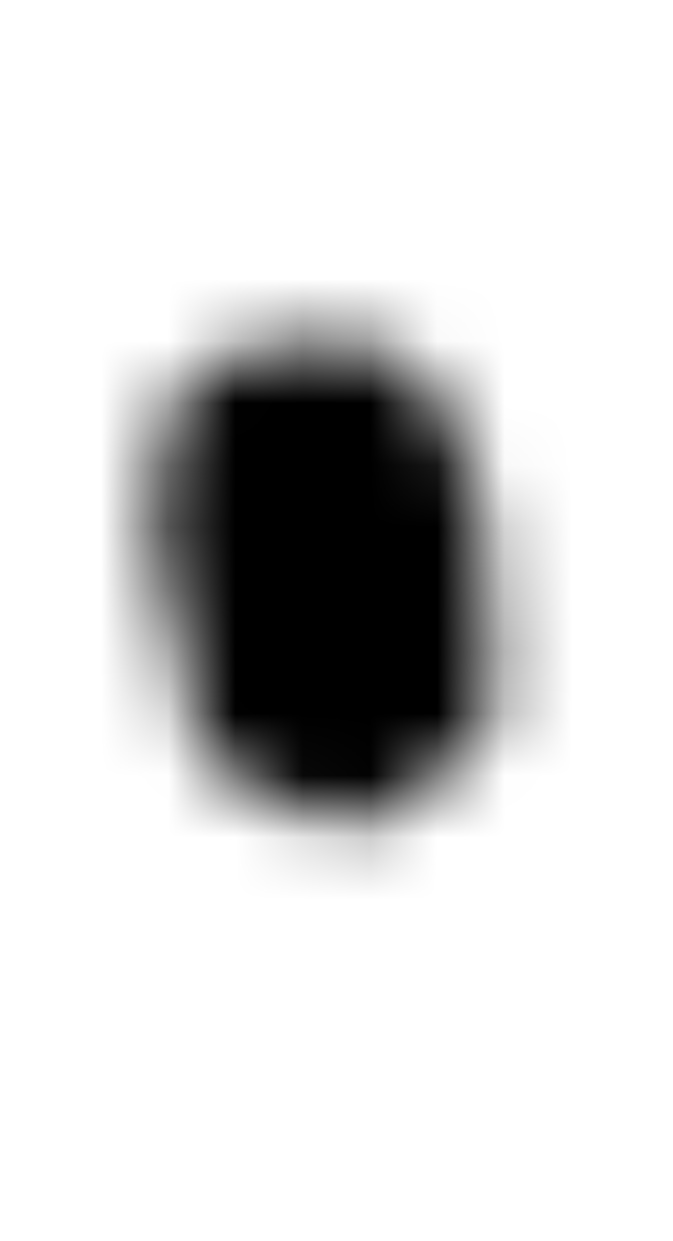
Did all part 2 in color.